
在今天,我们已经很清楚地知道,虽然事先无法确定某一个随机事件是否一定发生,但是可以依据一些先验信息来预测事件发生可能性的大小。比如,平时学习好的学生“期末考试得到90分以上”的可能性要大于平时学习不好的学生。特别是在信息时代的今天,随机事件更是充斥着人类活动的各个领域:人们的活动,包括上大学,找工作,生儿育女;社会的发展:包括GDP的增长,物价指数的变化,证券期货;现代科学研究:包括流行病的传播,遗传基因的表达,GPS定位系统,物理学中的不确定性原理,化学中的分子行为,语言学中的话语分类,计算机科学中图形识别,军事科学中的反导系统,航天科学中的卫星回收等等,数不胜数。那么,如何把这样一类问题抽象出来进行数学表达呢?我们还是从最简单的问题入手进行分析。
一个袋子里有五个大小一样的球,其中有四个白颜色的球和一个红颜色的球。 (1)
如果我们从上面的袋子里随机地摸一个球,那么,这个球是什么颜色的呢?显然,可能是白颜色的,也可能是红颜色的。这样,一个行为就可能有多个结果了,这与我们传统数学研究的函数是不一样的,因为函数要求“因变量取唯一值”。但是,我们还是能够利用抽象符号很好地表达“摸球”这个事件。仍然用y=f(x)来表示两个变量之间的关系,其中x表示摸球的行为,y表示摸到球的颜色。如果用1表示白球,用2表示红球,则y=1表示“摸到白球”这个事件发生,y=2表示“摸到红球”这个事件发生。我们称这种事先无法确定具体取值的变量y为随机变量,称一个随机事件发生的可能性的大小为概率,用P表示这个概率。因为现在白球多于红球,我们可以认为事件y=1发生的概率要大于事件y=2发生的概率,即P{y=1}>P{y=2}。如果假定每一个球被摸到的可能性都是一样大,容易得到
P{y=1}=4/5,P{y=2}=1/5
这样,我们可以给出计算概率的公式:
P{y=1}=白球的个数/所有球的个数
P{y=2}=红球的个数/所有球的个数
显然有:
0≤P{y=k}≤1,k=1,2;
P{y=1}+P{y=2}=1
这两条是概率必须满足的基本性质。
我们考虑更为复杂的情况,从而得到更为一般的结果。从袋子里有放回地随机摸两个球,那么,随机变量y可能得到下面四种情况之一:
白白,白红,红白,红红 (2)
如果我们只关心颜色而不关心得到颜色地顺序,那么,中有三种不同的情况:两个都是白球,一个白球一个红球,两个都是红球,分别用1,2,3来表示这三个事件,现在来计算概率。
先考虑一个简单的方法,因为摸一次球为白球的概率是4/5,那么连续摸两次得到的都是白球的概率就是(4/5)X(4/5)。同理,连续摸两次得到的都是红球的概率为(1/5)X(1/5)。然后根据概率的和为1的基本性质,可以得到一个白球一个红球的概率。这样有
P{y=1}=(4/5)X(4/5)=16/25
P{y=2}=(1/5)X(1/5)=1/25
P{y=3}=1-16/25-1/25=8/25
我们还可以用计算乘积事件的方法得到P{y=2}。用p表示一次摸球摸到白球的概率,用q=1-p表示一次摸球摸到红球的概率,那么摸到一个白球一个红球的概率为pXq,因为有白红和红白两种情况,应当为2倍,则有
{y=2}=2pq=2X(4/5)X(1/5)=8/25
最后,为了得到一般的公式,我们用直接计算的方法。先考虑从5个球中有放回地摸出2个球地所有可能,因为是有放回的,第一次被摸到的球第二次仍然有可能被摸到,因此有5X5=25种可能;再考虑摸到一个白球一个红球的所有可能,一个是从4个白球中摸出1个,有4种可能,一个是从1个红球中摸出1个,只有1中可能,因为有白红和红白两种情况,所有有2X4X1=8中可能。概率应当为这两种可能之比,就可以得到事件“摸到一个白球一个红球”发生的概率为8/25。这样,我们可以一般地定义事件{y=k}发生地概率为
P{y=k}=使得事件{y=k}发生地可能数/所有可能数 (3)
这个定义被称为概率的古典定义,是法国数学家拉普拉斯在他1812年的著作《概率的分析理论》中给出的。
为了使得问题更具条理性,从而给出更一般的结果,我们还需要对随机事件进一步抽象。首先定义事件之间的运算,把我们感兴趣的形式最为简单的事件称为基本事件,用wi表示,其中i=1,…,n(或者无穷)。令Ω={w1,…wn}表示由所有基本事件构成的集合,称其为样本空间。用字母A,B等表示样本空间Ω的子集合,即是由w1,…wn中部分事件构成的集合,称这样的子集合为事件。很显然,一个基本事件也是样本空间的一个子集合,因而构成事件。约定只要A中有一个基本事件发生则认为事件A发生。进一步,用
A⊂B表示w∈A,则w∈B,称为“B包含A”;
A∪B表示如果w∈A∪B则w∈A或者w∈B,称为“A与B的并”;
A∩B表示如果w∈A∪B则w∈A并且w∈B,称为“A与B的交”;
如果A∩B=∅,即A和B中没有共同包含的基本事件,则称“A与B互斥”;如果A与B互斥并且A与B的并为样本空间,即A∪B=Ω,则称“A与B互补”。
还是利用两次摸球的例子来直观说明这些运算。由(2)式可以得到样本空间Ω={白白,白红,红白,红红}。显然,A={白白},B={白白,白红,红白}和C={白红,红白,红红}都是Ω的子集,并且
A⊂B,A∪B=B,B∪C=Ω,A∩B=A,B∩C={白红,红白}。
因为A∪C=Ω和A∩C=∅,所有A与C互补。
现在我们就可以一般地定义事件发生的概率了。概率P是定义在样本空间Ω上的一个测度,这是一种对集合大小的度量,满足:
1. 非负性:对于Ω的任何子集A,由P(A)≥0;
2. 完全性:P(Ω)=1;
3. 可加性:如果A和B互斥,则P(A∪B)=P(A)+P(B)
通常称上述定义为概率的公理化定义。在这个非常一般的定义下,可以比较清晰地阐明概率论地许多重要定理和推导出许多重要的计算公式。这些基础性工作是20世纪最杰出的数学家之一,俄罗斯的柯尔莫洛夫创立的。他在1933年出版的德文著作《概率论基础》已经成为这个研究领域的经典。
上面的第3条是本质的。事实上,两个事件A和B的并A∪B构成了一个新的事件,如下图所示:
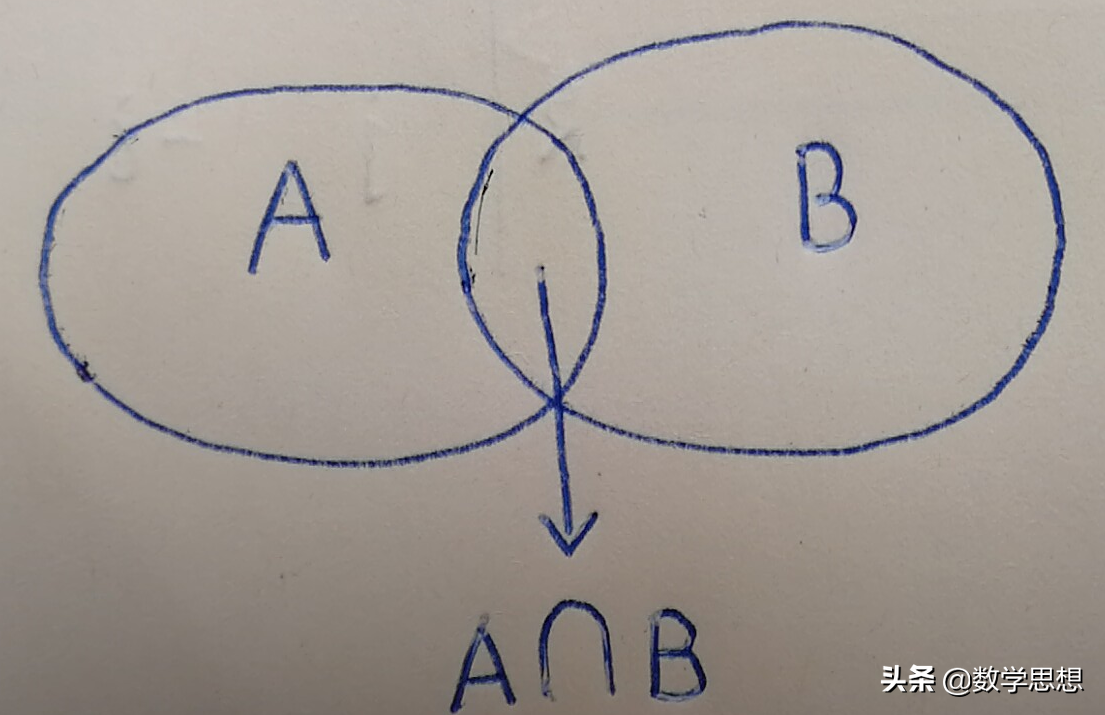
这个新的事件发生的概率,应当为事件A和事件B发生的概率之和减去事件A∩B的概率,即P(A∪B)=P(A)+P(B)-P(A∩B),这是因为在P(A)+P(B)中事件A∩B发生的概率被重复计算了两次,所有应当减去其中的一次。当A∩B=∅时,就有了第3条。由上式容易得到,如果A⊂B且A≠B时,有P(A)
与我们对数学的讨论一样,高度的抽象对于深刻理解数学的含义是重要的,但是也带来了一个非常打的弱点:高度的抽象是以丢弃直观为代价的。我们在上面的定义中,已经根本看不到随机性了,也体会不到随机事件可能发生也可能不发生的神秘感了。后续,我们将从一个全新的,几乎不能称其为数学的角度来分析这个问题。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需99元,全站资源免费下载 点击查看详情
站 长 微 信: hs105011





评论(1)